[masraum]

https://physics.stackexchange.com/questions/132935/gravity-beneath-sea-level

this sounds pretty good.

I'm assuming the question is "How does gravity vary inside the Earth?"

I'll look at this three ways:

From a rather empirical set of corrections used by geologists for work near the surface of the Earth,
From a physicist's spherical cow perspective, and finally,
From empirical data collected by geologists and geophysicists that give a better picture of gravitation inside the Earth.

Free air and Bouguer corrections

Linearizing Newton's law of gravitation ��=������2
about height at sea level yields ��(ℎ)=��0−2��0��earthℎ, or Δ����(ℎ)=−3.084×10−6s−2ℎ, where ℎ

is in meters. This is the free air correction. It yields an estimate for gravitational acceleration for a balloon flying a small distance above the Earth.

What if instead the intervening space was filled with some material with a density ��
? One way of accounting for that stuff is to pretend that it's an infinite flat of material. This leads to the Bouguer correction, ������(ℎ,��)=4.194×10−10m3kg−1s−2��ℎ, where �� is in kilograms per cubic meter and ℎ

is in meters.

That's for going above sea level. What about below? The free air correction still applies as-is (with height being negative). The Bouguer correction needs a correction. Since that correction is based on a flat plate model, gravity inside the Earth needs a double Bouguer correction.

Assuming sea water with a density of 1025 kg/m3, the above corrections leads to gravitational acceleration under the sea increasing by 2.224×10-6 m/s2 per meter of depth in sea water.
Earth as a sphere with density that varies radially

Per Newton's shell theorem, gravitation inside a sphere whose density depends only you radial distance from the center is given by ��(��)=����(��)��2
, in other words, it's just Newton's law of gravitation, but that ��(��) represents only the mass that is inside a sphere of radius ��

. The stuff above contributes nothing.

Differentiating with respect to distance ��
yields ��������=����3(����������−2��(��)). For a spherically symmetric object, ��������=4����(��)��2, where ��(��) is the density at a distance �� from the center of the Earth. Denoting the mean density ��¯(��) as ��¯(��)≡��(��)��(��)=��(��)4/3����3 lets us write ��(��)=43����¯��3. Applying these results to the expression for �������� yields ��������=4����(��(��)−23��¯(��)). We want the effects of increasing depth below the surface rather than increasing distance from the center. That's simple: Just negate the above:
��������=4����(23��¯(��)−��(��))
where ��

is depth below the surface.

Applying the above to sea water with a density of 1025 kg/m3 and using 5515 kg/m3 as the mean density of the Earth leads to gravitational acceleration under the sea increasing by 2.224×10-6 m/s2 per meter of depth in sea water, the same result as with the empirical models.
Gravitation inside the Earth

One thing pops right out from the physics-based derivation: Gravitational acceleration increases with increasing depth if the local density ��(��)
is less than 2/3 times the mean density ��¯(��) of all the stuff at a depth ��

or greater. It decreases if the local density is at least 2/3 of the mean density. Surface rock has a density a bit less than 1/2 the mean density of the Earth, so gravitational acceleration initially increases with increasing depth. In fact, gravitational acceleration inside the Earth is above the surface value until just below the core-mantle boundary. The global maximum occurs at the core-mantle boundary. The Earth's core is very, very dense stuff. It's mostly iron and it is highly compressed.

This is exactly what is seen in the Preliminary Reference Earth Model. Below are some links to the PREM.

Wikipedia article: http://en.wikipedia.org/wiki/Preliminary_reference_Earth_model

Model parameters: http://geophysics.ou.edu/solid_earth/prem.html

Paper: Dziewonski, A. M., & Anderson, D. L. (1981). "Preliminary reference Earth model." Physics of the earth and planetary interiors, 25(4), 297-356.

Finally, here's a graph of gravitational acceleration above and inside the Earth.

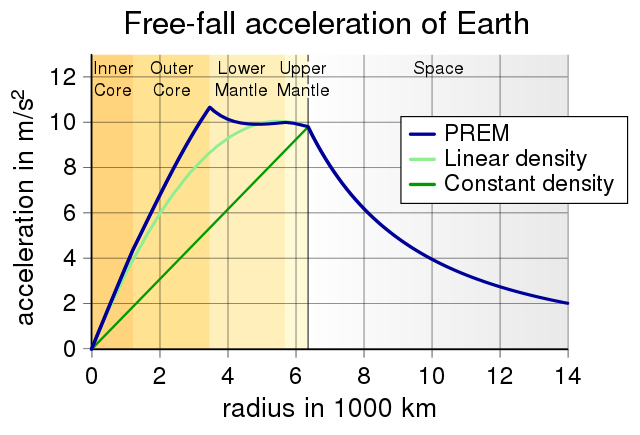
I guess if you want to see the equations, you'll have to follow the link. Interesting stuff.