Sad to say but not everyone teaching math has a complete grasp of all it's nuances
the pertinent property that is causing all the issues is one of the most basic, so basic that many just dash through it w/o truly appreciating its meaning
once again multiplication is associative as is addition, one can place parenthesis wherever one chooses thus altering the basic left to right rule, or leave the parenthesis off retaining the basic left to right rule, the result does not change, ie you have consistent results no matter how it's done.
(ab)c = a(bc) = abc and (a+b)+c = (a+b)+c = a+b+c
division and subtraction do not have the associative property, you can not place a parentheses affecting any division or subtraction in any expression that alters the rule left to right in any way.
(a/b)c is not equal to a/(bc) and (ab)/c is not equal to a(b/c)
In any expression containing division or subtraction you have to go in strict left to right order. If you do not then you get different results as we have seen here in this thread.
I demonstrated by alternate methods ie rationalizing, that strict left to right will give consistent results
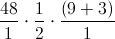
additionally the Parenthesis part of PEMDAS is apparently misunderstood. It says to do any operation inside a parenthesis if you can, in fact it is not necessary to do the inside of the parenthesis first as in this problem you can use the distributive property
additionally one of the more important basic properties of multiplying the coefficient outside a parentheses by the inside is that it clears the parenthesis. ie once you multiply the coefficient by the parenthesis the parenthesis is gone and cannot be reused
using the distributive property and going strictly left to right where the division is the first thing gives the following
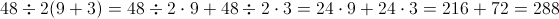
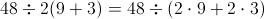 we go no further here because
we go no further here because another property has been violated, when a term outside the parentheses is multiplied by the parenthesis it clears the parenthesis from the expression if the parentheses is cleared as it ought to you get
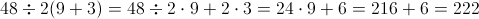
another inconsistent result