Quote:
Originally Posted by winders

|
again there is absolutely no ambiguity, there are only people that don't understand or follow the rules
from the link,
What is 2x/3y-1 if x=9 and y=2 ? the author argues 'It is not clear what the textbook had intended with the 3y' that is a specious argument as the solver must only consider what is written, again Math not ESP, 'One can however also argue that "3y" is a unit which belongs together.' again a specious argument designed to deflect responsibility from knowing the rules, 3y is a unit is nonsense, what is written is 3 multiplied by y
Further using the arguement that various computer programs give different results merely shows that the coder wrote faulty code
first note that there are no parenthesis, the
only way to add a parenthesis where one did not exist is to use the substitution principle as outlined below or where by adding the parenthesis the sense of the problem is not changed
an exaple of the latter is to rewrite 3x as 3(x)
so step 1 is to substitute equivalent values for the variables, the rule to do that is to first put parenthesis where the variable was
2( )/3( ) - 1 then fill the parenthesis w/ the equivalent value or equivalent expression.
2(9)/3(2) - 1 now eliminate the parenthesis by multiplication, this is part of the P in PEMDAS
18/6 - 1 now divide, this is the D in PEMDAS
3 - 1 now subtract
2
there alternate pedagogies to PEMDAS that do the same thing
one is to always isolate terms from each other and to simplify the terms in isolation, terms quite simply are separated from each other by + or - which are not inside a parenthesis or by comparatives like =, > or < etc.
using this method 2x/3y is considered in isolation
from there the same substitution principle is used and then since there is nothing to be done inside the parenthesis and the exponent on the parenthesis is 1 the next step is to multiple to remove each parenthesis. There is certainly a lack of full uderstanding by many about the full extent of the p in PEMDAS, limiting the discussion to only Algebra and excluding tri or other higher functions
P alone has several steps that are often not considered
step 1 of P is to do what you can inside the parenthesis, again this is done in isolation
step 2 is to do any exponents on the parenthesis, there is always an exponent even if it is only 1 which doesn't change anything most of the time so like extra parenthesis is rarley written for simplicity.
step 3 is to multiply the parenthesis bu it's numerical coefficient, as w/ the exponent 1 there is always a numerical coefficient even if it is 1 which again is often not written but which serves the very important function of eliminating the parenthesis from the problem
This expression shows the usually unwrtitten but understood 1's, here the exponent 1 does notheing but the coefficient 1 when miultiplied by using the distributive property eliminates the parenthesis
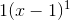
it is equivalent to
1(x - 1) and (x - 1) and x - 1
there is a third one that would be considered if this was a ratioanl expression, but since it's not I've ommited discussion of that
then the 2 terms are integrated to get the final answer